深度学习评估指标

1 AUC

AUC，即曲线下面积（Area Under the Curve），通常用于评估二分类模型的性能。它主要基于ROC曲线（受试者操作特征曲线）来计算，ROC曲线展示了在不同阈值下模型的敏感性与特异性之间的关系。AUC值范围从0到1，值接近1表示模型的分类效果越好。

1.1 ROC(Receiver Operating Characteristic)曲线

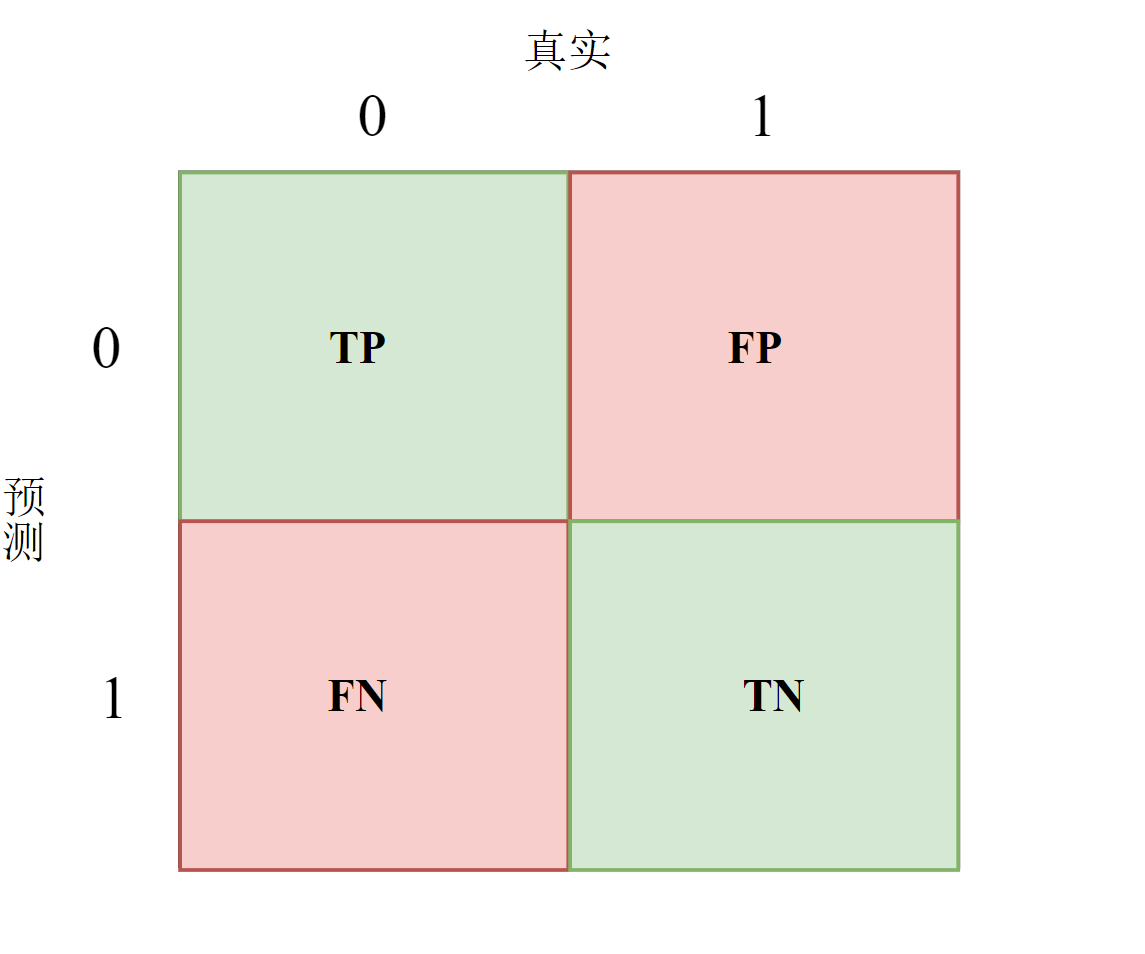
1. FPR为假阳率（False Positive Rate），即模型预测为正例的样本中实际为负例的比例。

\[ FPR = \frac{FP}{N} = \frac{N_0}{N} \]

上式中，\(N_0\)为实际为负例的样本数，\(N\)为总样本数。

2. TPR为真阳率（True Positive Rate），即模型预测为正例的样本中实际为正例的比例。

\[ TPR = \frac{TP}{P} = \frac{N_1}{N} \]

上式中，\(N_1\)为实际为正例的样本数，\(P\)为正例的样本总数。

3. 对角线对应于随机猜测模型，曲线越接接近左上角，分类器的性能越好。
4. ROC曲线的绘制
   1. 根据每个测试样本属于正样本的概率值从大到小排序；
   2. 从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本；
   3. 每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。

当我们将threshold设置为1和0时，分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来，就得到了ROC曲线。当threshold取值越多，ROC曲线越平滑。

1.2 AUC

AUC越接近1，分类器性能就越好

我们想要模型尽可能在将样本预测落入图中的绿色区域，即TPR=1，FPR=0，当TPR=FPR时，这将表明模型对于预测正负类都会预测错误一半的样本，此时可视作随机猜测模型。而我们的愿望是TPR>FPR，此时的ROC曲线将会处于对角线的上方，此时AUC的值较大，其内在含义是模型预测正确正样本的能力优于随机猜测模型。

AUC的排序特性

例如0.9的AUC，其含义可以大概理解为：给定一个正样本和一个负样本，在90%的情况下，模型对正样本的打分高于对负样本的打分。可以看出在这个解释下，我们关心的只是正负样本之间的分数高低，而具体的分值则无关紧要。

1.2.1 AUC的统计学含义

记 \(\text{TPR}(t)=\text{P}(s(x^+)\ge t)\) 为真阳率，\(\text{FPR}(t)=\text{P}(s(x^-)\ge t)\) 为假阳率，\(t\) 为阈值， \(s(\cdot)\) 为模型的得分函数，\(x^+, x^-\) 为正负样本，则AUC为：

\[ AUC = \int_{1}^0 \text{TPR}(t) d\text{FPR}(t) \]

由于得分函数 \(s(\cdot)\) 是一个连续函数，故有 \(\text{FPR}(t)=1-\text{P}(s(x^-)\le t)=1-F_-(t)\) ，其中 \(F_-(t)=P(s(x^-)\le t)\)，同理有 \(F_+(t)=P(s(x^+)\le t)\)。故AUC可以写成：

\[ \begin{align*} AUC &= \int_{1}^0 \text{TPR}(t) d\text{FPR}(t) \\ &= \int_{1}^0 \text{TPR(t)} d(1-F_-(t))\\ &= \int_{0}^1 \bigl[\int_0^1 I\{s^+\ge t\} dF_+(s^+)\bigr] d F_-(t) \\ &= \int_{0}^1 \bigl[\int_0^1 I\{s^+\ge t\} dF_-(t)\bigr] d F_+(s^+) \\ &= \int_{0}^1 \bigl[\int_0^{s^+} dF_-(t)\bigr] d F_+(s^+) \\ &= \int_{0}^1 \bigl[\int_0^{s^+} dF_-(s^-)\bigr] d F_+(s^+) \\ &=\text{P}(s(x)^-\leq s(x)^+) \end{align*} \]

上述证明即可表明，AUC的统计学上的含义是，所有随机抽取一对正负样本，正样本的得分大于负样本的概率。

1.3 AUC指标在推荐系统中应用存在的问题 ¹

1. 为什么点击率模型的auc要低于购买转化率模型的auc？

   因为点击率行为的成本低于购买成本——对于不喜欢的东西，相较于购买，用户更有可能会点击导致点击率模型的正负样本的差别小于购买率模型，因此点击率模型的auc要低于购买转化率模型的auc。

2. AUC值本身的理论上限

   即使拥有一个强大的模型，其AUC值也不能为1，因为现实中存在大量的歧义样本——特征集合完全一致，但标签不同。因此当拿到样本数据是，我们应当先去查看歧义样本所占的比例，并在进行特征工程时考虑由歧义样本造成的误差（Bayes Error Rate)，以此作为特征构建的一个参考指标。

3. AUC与线上业务指标的宏观关系

   样本数据包含的详细越接近线上，则离线指标与线上指标之间的差距就越小。而当决策链路越长，信息丢失的越多，则更难做到线下线上一致（例如：用户在我们的平台看到了一个产品但在另一个平台看见了更便宜的或者在一些评测文章中不被推荐等原因，这些信息我们无法收集到，导致最终的样本包含的信息确实较大，从而使得线下指标与线上指标之间的差距大）。

4. AUC提升和业务指标不一致

   若AUC指标显示较老模型有所提升，但是未看到AB测试中点击率也同步提升，则可能存在以下问题：

   • 排除BUG：线上线下的模型的预测的结果都要符合预期。
   • 谨防样本穿越：防止测试集的信息流入训练集当中。

5. AUC指标的不足

   • 线上会出现新样本，在线下没有见过，造成AUC不足。这部分更多是采用online learning的方式去缓解，AUC本身可改进的不多。
   • 线上的排序发生在一个用户下，而线下计算全集AUC，即把用户1点击的正样本排序高于用户2未点击的负样本是没有实际意义的，但线下AUC计算的时候考虑了它。

Footnotes

1. https://mp.weixin.qq.com/s/e3qcSo8LPDf2S8TUvU6S1A?poc_token=HPUzD2ijl0y_glmkNHQjkQHeRX3QnIydQdSuiRQJ